Parameters

• Body mases: \( m_1=m_2=m_3=1 \)
  
• Newton's gravitational constant: \( G=1 \)
  
  

Shape Space Sphere

Shape of the triangle is uniquely defined by following unit three-vector: \begin{eqnarray} {\hat {\vec n}} &=& (n_x^{'},n_y^{'},n_z^{'}) = \left(\frac{2 {\vec \rho} \cdot {\vec \lambda}}{R^2}, \frac{\lambda^2 - \rho^2}{R^2}, \frac{2 ({\vec \rho} \times {\vec \lambda}) \cdot \vec e_z}{R^2} \right),\ \end{eqnarray} where \begin{eqnarray} {\vec \rho} &=& \frac{1}{\sqrt{2}}({\vec x_1} - {\vec x_2}),\\[1mm] {\vec \lambda}&=& \frac{1}{\sqrt{6}}({\vec x_1} + {\vec x_2}- 2 {\vec x_3}). \end{eqnarray} are the Jacobi three-body coordinates and \( R \) is "overall size" of the system (hyper-radius): \begin{equation} R = \sqrt{\rho^{2} + \lambda^{2}}. \end{equation} A point on the shape sphere together with hyper-radius defines the configuration space of the three-body problem, up to rotations and translations.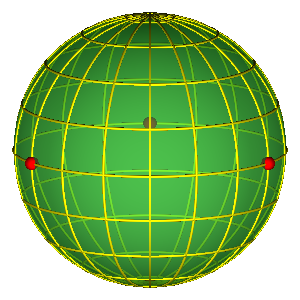 Equator of the shape sphere is related to the colinear configuratins (syzygies), while red dots are related to the three two-body collision points. The equator divides the shape sphere into two hemispheres with two opposite triangle orientations.

Classification of periodic solutions

Three-body orbits (periodic solutions) can be classified as closed curves (loops) on the shape-space with three punctures (singularities of the potential) using topological homotopy. Topological description of an orbit is given by the coresponding conjugacy class of the fundamental group of a two-sphere with three punctures. Graphically, this amounts to classifying closed curves according to their "topologies" on a sphere with three punctures. A stereographic projection of this sphere onto a plane, using one of the punctures as the "north pole" effectively removes that puncture to infinity, and reduces the problem to one of classifying closed curves in a plane with two punctures. That leads to the aforementioned free group on two letters \( (a,b) \), where (for definiteness) \( a \) denotes a clockwise "full turn/circle" around the right-hand-side puncture, and \( b \) denotes the counter-clockwise full turn/circle around the other pole/hole/puncture in the plane/sphere.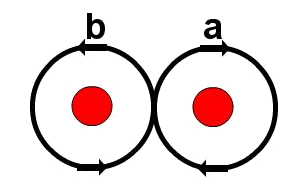 For better legibility we denote their inverses by capitalized letters \( a^{-1}=A \) and \( b^{-1}=B \). Each family of orbits is associated with the conjugacy class of a free group element. For example the conjugacy class of \( aB \) contains \( A(aB)a = Ba \), corresponding to the same orbit.

<<< BACK TO THE GALLERY